Research Design 1: Fixed Effects and Instrumental Variables
Stijn Masschelein
Did we not cover that already?
Yes, but briefly
Yes, but starting from the perspective of a regression (and the code)
Research Design
The focus is on Research Design
Important
- Which data should we use?
- Which comparison identifies the effect that we are interested in?
Prevously, we used models and assumptions to identify effects
Mathematical models
V=TαT(KαK)αK(LαL)αL αT+αK+αL=1
- V= The value of the firm
- K= Capital of the firm
- L= Labour of the firm
- T= CEO talent/skills/ability/experience
DAGs
Just focus on a setting where we are confident in the assumptions
Actual random assignment
Speedboat racing, game shows, Vietnam draft
Natural experiments
See Gippel, Smith, and Zhu (2015), Chapter 19 Instrumental Variables in Huntington-Klein (2021)
Policy Changes
Chapter 18, Difference-in-Difference in Huntington-Klein (2021)
Discrete cutoffs
e.g. WAM > 75, Chapter 20 Regression Continuity Design in Huntington-Klein (2021)
Unexpected news
Chapter 17 Event Studies in Huntington-Klein (2021)
Look for these designs!
- Based on your understanding of the industry and setting or the Data Generating Process
- When you read good papers for this unit and other units.
What is this effect?
What effect can we identify?
Average Treatment Effect
Average Treatment on the Treated
Average Treatment on the Untreated
Local Average Treatment Effect
Weigthed Average Treatment Effect
Chapter 10, Treatment Effects in Huntington-Klein (2021)
It all depends on where the variation is coming from.
Warning
Different firms react differently and are differently represented in the control group and the treatment group.
Note
- With actual random assignment, you probably have an ATE for the population that received the assignment.
- If you can use a control group because that is what the treated group would look like if they were not treated, you probably have an ATT.
- If you use a natural experiment to identify part of the variation, you probably have a LATE.
Chapter 10, Treatment Effects in Huntington-Klein (2021)
Why do we care?
Research Design
There is a deep connection between the variation in your research design and the effect you can identify.
Policy Implications
Whether your study has implications for “regulators and investors” depends heavily on the type of effect you can identify.
Chapter 10, Treatment Effects in Huntington-Klein (2021)
A simulated example
Generate the Data
N <- 1000
rd1 <- tibble(
firm = 1:N,
high_performance = rbinom(N, 1, 0.5),
noise = rnorm(N, 0, 3)
) %>%
mutate(
donation = high_performance,
performance = ifelse(high_performance == 1, 4, 1),
payoff_donation = 4 - 8 / performance + noise,
payoff_no_donation = 1 + noise
)
glimpse(rd1) Rows: 1,000
Columns: 7
$ firm <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …
$ high_performance <int> 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1…
$ noise <dbl> -0.3270031, -6.3484068, -1.5208…
$ donation <int> 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1…
$ performance <dbl> 4, 1, 1, 1, 4, 1, 1, 1, 4, 1, 4…
$ payoff_donation <dbl> 1.6729969, -10.3484068, -5.5208…
$ payoff_no_donation <dbl> 0.6729969, -5.3484068, -0.52088…Have a look at the data
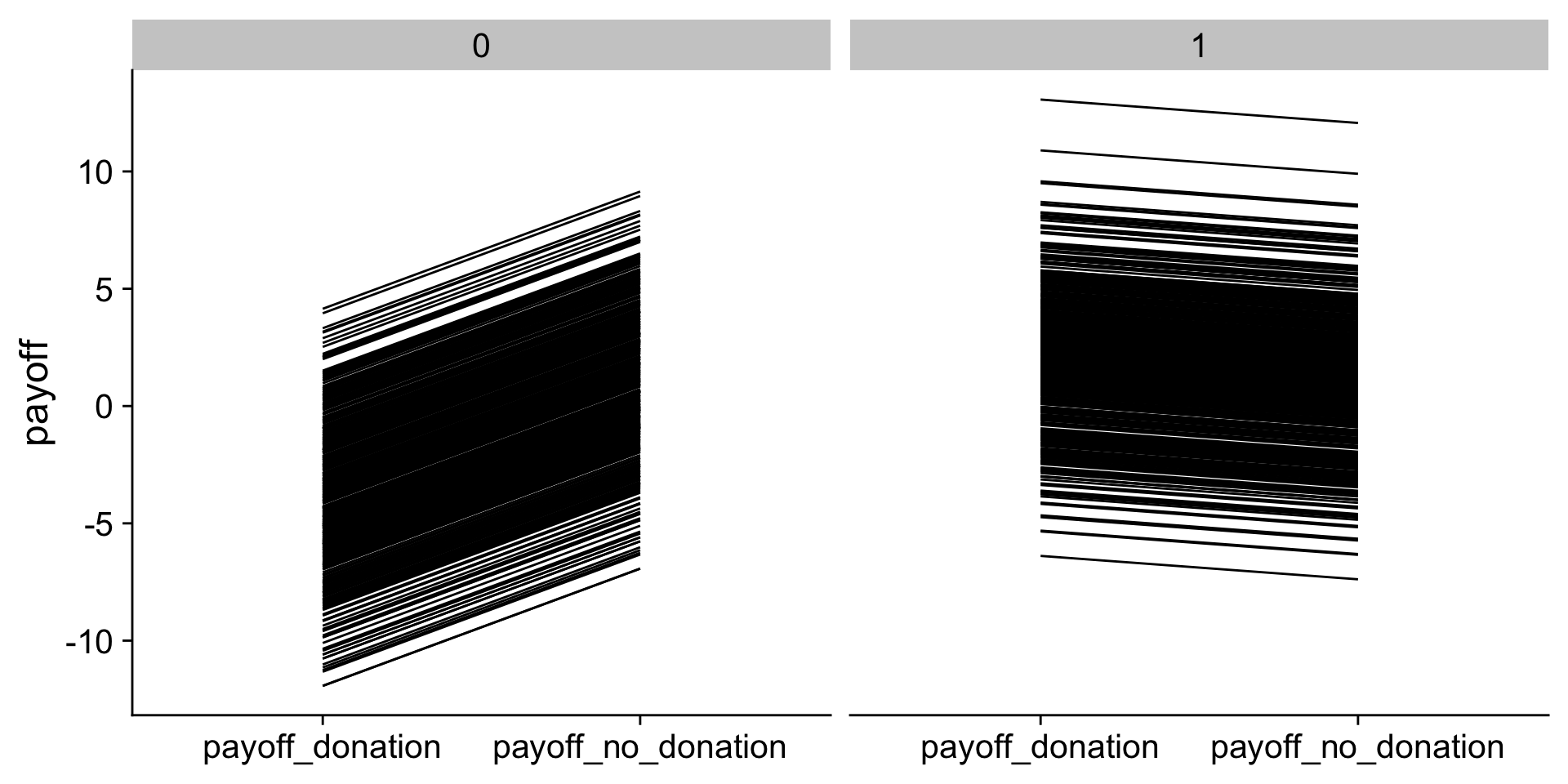
Have a second look at the data
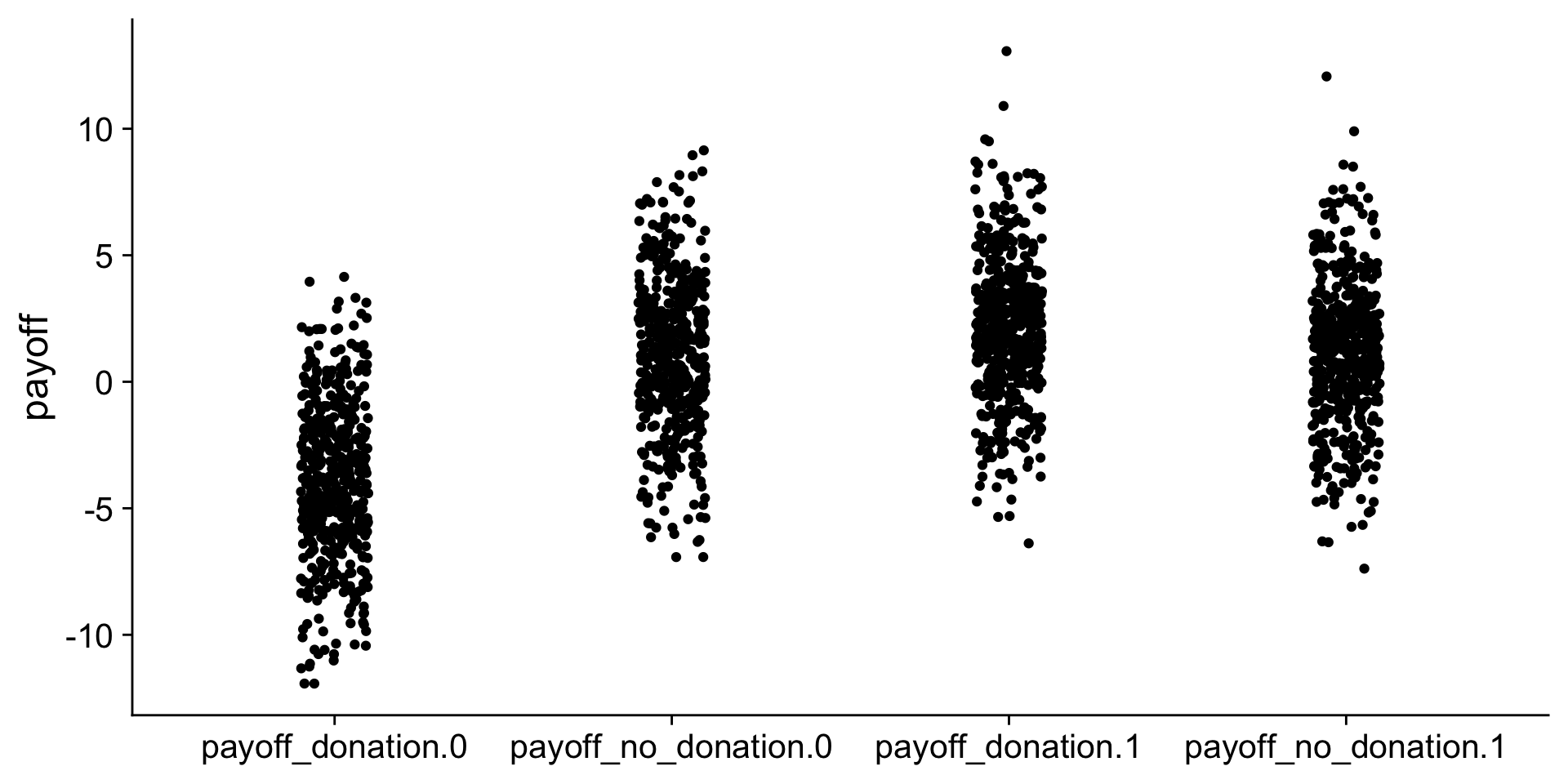
Real data does not have the counterfactuals. We only observe blue!
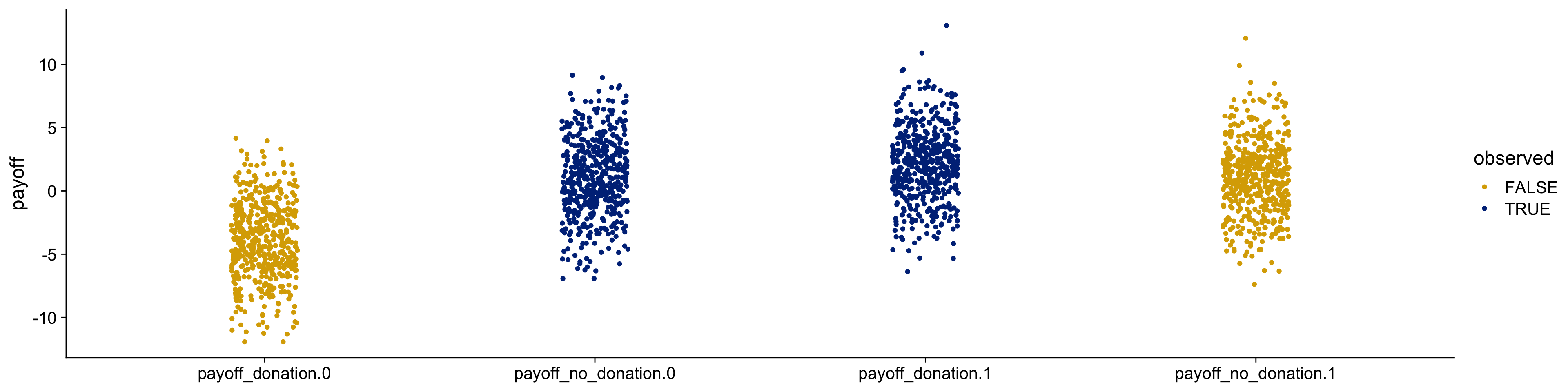
Note
The actual sample determines which comparisons we can make.
Let’s redo the simulated example with averages
Let’s redo the simulated example with averages
| M_causal | sd_causal | N |
|---|---|---|
| -1.98 | 3 | 1000 |
Let’s redo the regression with averages
summary_data <- rd1 %>%
group_by(donation) %>%
summarise(M_payoff_donation = mean(payoff_donation),
M_payoff_no_donation = mean(payoff_no_donation))
knitr::kable(summary_data, format = "markdown", digits = 2)| donation | M_payoff_donation | M_payoff_no_donation |
|---|---|---|
| 0 | -3.94 | 1.06 |
| 1 | 2.13 | 1.13 |
Note
- The true ATT is 1
- The effect estimated by the regression is 1.071
If you do not believe me, here is the regression
What could possibly go wrong?
Causal Effect Estimates with a Confounder
summary_data <- rd2 %>%
group_by(donation) %>%
summarise(M_payoff_donation = mean(payoff_donation),
M_payoff_no_donation = mean(payoff_no_donation))
knitr::kable(summary_data, format = "markdown", digits = 2)| donation | M_payoff_donation | M_payoff_no_donation |
|---|---|---|
| 0 | -3.93 | 2.07 |
| 1 | 2.02 | 1.02 |
- The true ATT is 1
- The effect estimated by the regression is -0.047
A Simulated Example of Panel Data
Note
- We want to use the counterfactual as the control group
- Panel data + fixed effects is the next best thing
Where is the variation coming from?
We need firms that make mistakes
- Firms that should donate but do not always do it.
- Firms that should not donate but sometimes donate.
Panel Data Simulation (100 firms)
N <- 100
rd_firm <- tibble(
firm = 1:N,
high_performance = rbinom(N, 1, 0.5),
other_payoff = rnorm(N, 0, 3)) %>%
mutate(
donation = high_performance,
performance = ifelse(high_performance == 1, 4, 1),
payoff_no_donation = ifelse(high_performance == 1, 1, 2) + other_payoff,
payoff_donation = 4 - 8/performance + other_payoff
)
summary_data <- rd_firm %>%
group_by(donation) %>%
summarise(M_payoff_donation = mean(payoff_donation),
M_payoff_no_donation = mean(payoff_no_donation))
knitr::kable(summary_data, digits = 1)| donation | M_payoff_donation | M_payoff_no_donation |
|---|---|---|
| 0 | -4.2 | 1.8 |
| 1 | 2.3 | 1.3 |
Panel Data Simulation (10 time periods)
The variation comes from high performers not donating some years
T <- 10 rd_panel_forget <- tibble( firm = rep(1:N, each = T), year = rep(1:T, times = N)) %>% left_join(rd_firm, by = "firm") %>% mutate(forget_donation = rbinom(N * T, 1, plogis(-other_payoff)), actual_donation = (1 - forget_donation) * donation, actual_payoff = ifelse(actual_donation == 1, payoff_donation, payoff_no_donation))T <- 10 rd_panel_forget <- tibble( firm = rep(1:N, each = T), year = rep(1:T, times = N)) %>% left_join(rd_firm, by = "firm") %>% mutate(forget_donation = rbinom(N * T, 1, plogis(-other_payoff)), actual_donation = (1 - forget_donation) * donation, actual_payoff = ifelse(actual_donation == 1, payoff_donation, payoff_no_donation))T <- 10 rd_panel_forget <- tibble( firm = rep(1:N, each = T), year = rep(1:T, times = N)) %>% left_join(rd_firm, by = "firm") %>% mutate(forget_donation = rbinom(N * T, 1, plogis(-other_payoff)), actual_donation = (1 - forget_donation) * donation, actual_payoff = ifelse(actual_donation == 1, payoff_donation, payoff_no_donation))T <- 10 rd_panel_forget <- tibble( firm = rep(1:N, each = T), year = rep(1:T, times = N)) %>% left_join(rd_firm, by = "firm") %>% mutate(forget_donation = rbinom(N * T, 1, plogis(-other_payoff)), actual_donation = (1 - forget_donation) * donation, actual_payoff = ifelse(actual_donation == 1, payoff_donation, payoff_no_donation))
The New Assignment
- Run a fixed effect model and interpret the result
- Create a new dataset where all firms make mistakes
- Run a fixed effect model and interpret the result
Instrumental Variable Approach
Causal Diagram
Causal Diagram
See Instrumental Variables, Chapter 19 in Huntington-Klein (2021).
Simulation and Implementation with fixest
#|label: simulation-iv
d <- tibble(
iv = rnorm(N, 0, 1),
confounder = rnorm(N, 0, 1)) %>%
mutate(
x = rnorm(N, .6 * iv - .6 * confounder, .6),
y = rnorm(N, .6 * x + .6 * confounder, .6),
survival = if_else(y > 0, 1, 0)
)
surv <- filter(d, survival == 1)
lm1 <- lm(y ~ x, d)
lm2 <- lm(y ~ x + confounder, d)
lm3 <- lm(y ~ x, surv)
lm4 <- lm(y ~ x + confounder, surv)
iv1 <- feols(y ~ 1 | 0 | x ~ iv, data = d)
iv2 <- feols(y ~ 1 | 0 | x ~ iv, data = surv)Simulation results with a real effect of 0.6
msummary(list("confounded" = lm1, "with control" = lm2, "collider" = lm3, "collider" = lm4,
"iv no collider" = iv1, "iv with collider" = iv2),
gof_omit = gof_omit, stars = stars)| confounded | with control | collider | collider | iv no collider | iv with collider | |
|---|---|---|---|---|---|---|
| * p < 0.1, ** p < 0.05, *** p < 0.01 | ||||||
| (Intercept) | 0.102 | 0.022 | 0.658*** | 0.444*** | 0.125 | 0.517*** |
| (0.075) | (0.057) | (0.078) | (0.087) | (0.090) | (0.129) | |
| x | 0.308*** | 0.692*** | 0.133 | 0.440*** | ||
| (0.077) | (0.072) | (0.098) | (0.115) | |||
| confounder | 0.610*** | 0.360*** | ||||
| (0.068) | (0.090) | |||||
| fit_x | 0.794*** | 0.549* | ||||
| (0.165) | (0.293) | |||||
Simulation without an effect
d <- tibble(
iv = rnorm(N, 0, 1),
confounder = rnorm(N, 0, 1)) %>%
mutate(
x = rnorm(N, .6 * iv - .6 * confounder, .6),
y = rnorm(N, .6 * confounder, .6),
survival = if_else(y > 0, 1, 0)
)
surv <- filter(d, survival == 1)
lm1 <- lm(y ~ x, d)
lm2 <- lm(y ~ x + confounder, d)
lm3 <- lm(y ~ x, surv)
lm4 <- lm(y ~ x + confounder, surv)
iv1 <- feols(y ~ 1 | 0 | x ~ iv, data = d)
iv2 <- feols(y ~ 1 | 0 | x ~ iv, data = surv)Simulation without an effect
msummary(list("confounded" = lm1, "with control" = lm2, "collider" = lm3, "collider" = lm4,
"iv no collider" = iv1, "iv with collider" = iv2),
gof_omit = gof_omit, stars = stars)| confounded | with control | collider | collider | iv no collider | iv with collider | |
|---|---|---|---|---|---|---|
| * p < 0.1, ** p < 0.05, *** p < 0.01 | ||||||
| (Intercept) | -0.045 | -0.067 | 0.690*** | 0.530*** | -0.016 | 0.713*** |
| (0.084) | (0.070) | (0.070) | (0.075) | (0.090) | (0.076) | |
| x | -0.168** | 0.124 | -0.041 | 0.046 | ||
| (0.082) | (0.080) | (0.071) | (0.067) | |||
| confounder | 0.592*** | 0.302*** | ||||
| (0.087) | (0.080) | |||||
| fit_x | 0.099 | 0.030 | ||||
| (0.139) | (0.109) | |||||
Example:Sitting Duck Governors by Falk and Shelton (2018)
Note
- Research Question: Does political uncertainty effect investment?
- More uncertainty in a state when governor does not come up for reelection.
- State level laws with term limits (~ Random)
Data
library(readit)
duck <- readit(here("data", "LameDuckData.dta")) %>%
select(-starts_with("nstate"), -starts_with("stdum"),
-starts_with("yd_alt")) %>%
group_by(statename) %>%
arrange(year) %>%
mutate(log_I_1 = lag(log_I), log_I_2 = lag(log_I, 2),
log_Y_1 = lag(log_Y), log_Y_2 = lag(log_Y, 2),
log_real_GDP_1 = lag(log_real_GDP),
log_real_GDP_2 = lag(log_real_GDP, 2)) %>%
ungroup() %>%
arrange(statename) %>%
filter(year >= 1967, year <= 2004)Reduced Form
2 Stage Least Squares (2SLS)
Results
coef_map = c("gov_exogenous_middling" = "lame duck governor",
"fit_uncertainty_continuous" = "uncertainty")
msummary(list("reduced" = red_reg,
"first stage iv" = summary(iv_reg, stage = 1),
"second stage iv" = iv_reg),
gof_omit = gof_omit, stars = stars,
coef_map = coef_map)| reduced | first stage iv | second stage iv | |
|---|---|---|---|
| * p < 0.1, ** p < 0.05, *** p < 0.01 | |||
| lame duck governor | -0.049** | 1.801*** | |
| (0.021) | (0.112) | ||
| uncertainty | -0.027** | ||
| (0.012) | |||
Diagnostics: Test for endogeneity (Durbin-Wu-Hausmann)
Note
Is the IV result different from the OLS result?
summ_iv <- summary(iv_reg)
summ_1st <- summary(iv_reg, stage = 1)
summ_iv$iv_wh$stat # iv wu hausmann[1] 3.829033[1] 0.05054677Instrumental Variables, Chapter 19 in Huntington-Klein (2021)
Diagnostics: Test for weak instrument
Note
Is the instrument predicting the variable we want it to predict?
New Assignment
Let’s assume that firms are less likely to donate when there is a local election
N <- 5000 rd_iv_el <- tibble( high_performance = rbinom(N, 1, .5), extra_payoff = rnorm(N, 0, 3), local_election = rbinom(N, 1, .33)) %>% mutate( actual_donation = ifelse(high_performance == 1, 1 - local_election, 0), payoff_donation = ifelse(high_performance == 1, 2, - 4) + extra_payoff, payoff_no_donation = ifelse(high_performance == 1, 1, 2) + extra_payoff, actual_payoff = ifelse(actual_donation == 1, payoff_donation, payoff_no_donation))N <- 5000 rd_iv_el <- tibble( high_performance = rbinom(N, 1, .5), extra_payoff = rnorm(N, 0, 3), local_election = rbinom(N, 1, .33)) %>% mutate( actual_donation = ifelse(high_performance == 1, 1 - local_election, 0), payoff_donation = ifelse(high_performance == 1, 2, - 4) + extra_payoff, payoff_no_donation = ifelse(high_performance == 1, 1, 2) + extra_payoff, actual_payoff = ifelse(actual_donation == 1, payoff_donation, payoff_no_donation))
A Published IV example
How Do Quasi-Random Option Grants Affect CEO Risk-Taking? by Shue and Townsend (2017) in The Journal of Finance
This paper is a finished product, your pitch, proposal, or dissertation is not.
We are grateful to Michael Roberts (the Editor), the Associate Editor, two anonymous referees, Marianne Bertrand, Ing-Haw Cheng, Ken French, Ed Glaeser, Todd Gormley, Ben Iverson (discus- sant), Steve Kaplan, Borja Larrain (discussant), Jonathan Lewellen, Katharina Lewellen, David Matsa (discussant), David Metzger (discussant), Toby Moskowitz, Candice Prendergast, Enrichetta Ravina (discussant), Amit Seru, and Wei Wang (discussant) for helpful suggestions. We thank seminar participants at AFA, BYU, CICF Conference, Depaul, Duke, Gerzensee ESSFM, Harvard, HKUST Finance Symposium, McGill Todai Conference, Finance UC Chile, Helsinki, IDC Herzliya Finance Conference, NBER Corporate Finance and Personnel Meetings, SEC, Simon Fraser Uni- versity, Stanford, Stockholm School of Economics, University of Amsterdam, UC Berkeley, UCLA, and Wharton for helpful comments. We thank David Yermack for his generosity in sharing data. We thank Matt Turner at Pearl Meyer, Don Delves at the Delves Group, and Stephen O’Byrne at Shareholder Value Advisors for helping us understand the intricacies of executive stock option plans. Menaka Hampole provided excellent research assistance. We acknowledge financial support from the Initiative on Global Markets.
This paper has 1 (one!) research question. This is a good thing!
Do increases in option grants increase risk taking?
IV 1: Scheduled Discrete Increases in Fixed-Value Option Grants
For our first instrument, we use fixed-value firms, for which option grants can increase only at regularly prescheduled intervals (i.e., when new cycles start). For example, consider a fixed-value firm on regular three-year cycles. Other time-varying factors may drive trends in risk for this firm. However, these trends are unlikely to coincide exactly with the timing of when new cycles are scheduled to start.
IV 2: Within Cycle Grant Increases due to Industry Shocks in Fixed-Number Option Grants
For our second instrument, we focus on fixed-number firms. The value of options granted in any particular year varies with aggregate returns within a fixed-number cycle. This means that the timing of increases in option pay within a cycle will be random in the sense that the increases are driven in part by industry shocks that are beyond the control of the firm and are largely unpredictable. To account for the possibility that aggregate returns can directly affect risk, we use fixed-value firms as a control group because their option compensation must remain fixed despite changes in aggregate returns.
The authors know their setting!
Our identification strategy builds on Hall’s (1999)) observation that firms often award options according to multiyear plans. Two types of plans are commonly used: fixed-number and fixed-value. Under a fixed-number plan, an executive receives the same number of options each year within a cycle. Under a fixed-value plan, an executive receives the same value of options each year within a cycle.
Our conversations with leading compensation consultants suggest that multiyear plans are used to minimize contracting costs, as option compensation only has to be set once every few years. Hall (1999, p. 97) argues that firms sort into the two types of plans somewhat arbitrarily, observing that “Boards seem to substitute one plan for another without much analysis or understanding of their differences.”
Key Assumption 1 - Relevance: IV is related to Option Grants
We find that the first-year indicator corresponds to a 15% larger increase in the Black-Scholes value of new option grants than in other years.
All estimates are highly significant, with F-statistics greatly exceeding 10, the rule of thumb threshold for concerns related to weak instruments (Staiger and Stock (1997). (III A.)
Chapter 19 Instrumental Variables in Huntington-Klein (2021)
Key Assumption 2 - Exclusion (or validity): Only path from IV to Risk Taking is through Option Grants.
One might be concerned that predicted first years provide exogenously timed but potentially anticipated increases in option compensation. However, this is not an issue for our empirical strategy. […] He would have no incentive to increase risk prior to an anticipated increase in the value of his option compensation next period.
In addition, we directly examine whether fixed-value cycles appear to be correlated with other firm cycles […]
Chapter 19 Instrumental Variables in Huntington-Klein (2021)
One Criticism
First, option compensation tends to follow an increasing step function for executives on fixed-value plans. This is because compensation tends to drift upward over time, yet executives on fixed-value plans cannot experience an upward drift within a cycle.
While these two stylized facts do not hold in all cases—as can also be seen in Figure 1—our identification strategy only requires that they hold on average.
Some more terminology
- Compliers
- Always-takers/never-takers
- Defiers
Chapter 19 Instrumental Variables in Huntington-Klein (2021)
References
Falk, Nathan, and Cameron A. Shelton. 2018. “Fleeing a Lame Duck: Policy Uncertainty and Manufacturing Investment in US States.” American Economic Journal: Economic Policy 10 (4): 135–52. https://doi.org/10.1257/pol.20160365.
Gippel, Jennifer, Tom Smith, and Yushu Zhu. 2015. “Endogeneity in Accounting and Finance Research: Natural Experiments as a State-of-the-Art Solution.” Abacus 51 (2): n/a–. https://doi.org/10.1111/abac.12048.
Huntington-Klein, Nick. 2021. The Effect: An Introduction to Research Design and Causality. First. Boca Raton: Chapman and Hall/CRC. https://doi.org/10.1201/9781003226055.
Shue, Kelly, and Richard R. Townsend. 2017. “How Do Quasi-Random Option Grants Affect CEO Risk-Taking?” The Journal of Finance 72 (6): 2551–88. https://doi.org/10.1111/jofi.12545.
Research Design 1: Fixed Effects and Instrumental Variables Stijn Masschelein