RN <- 1000
random <- tibble(
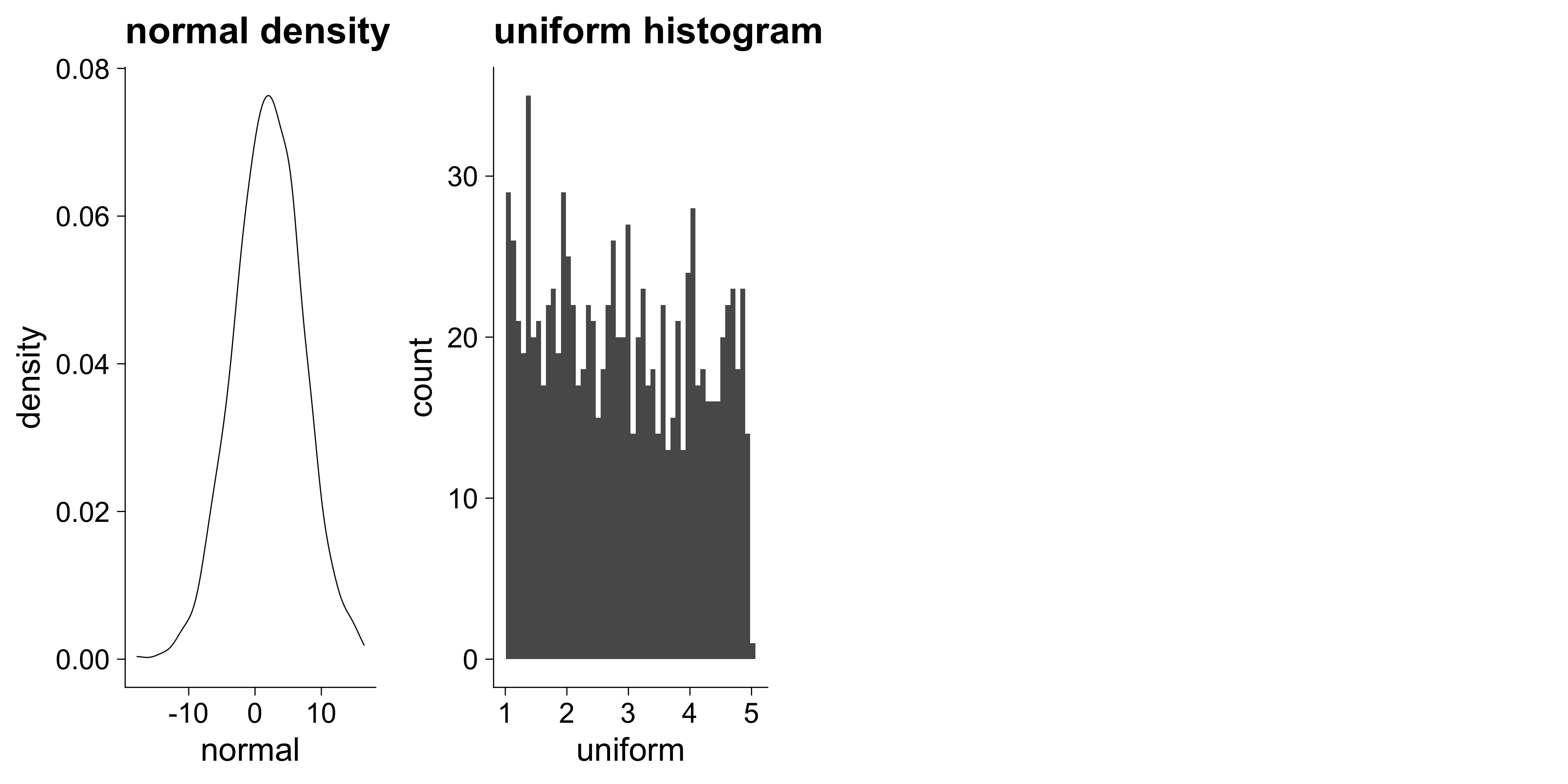
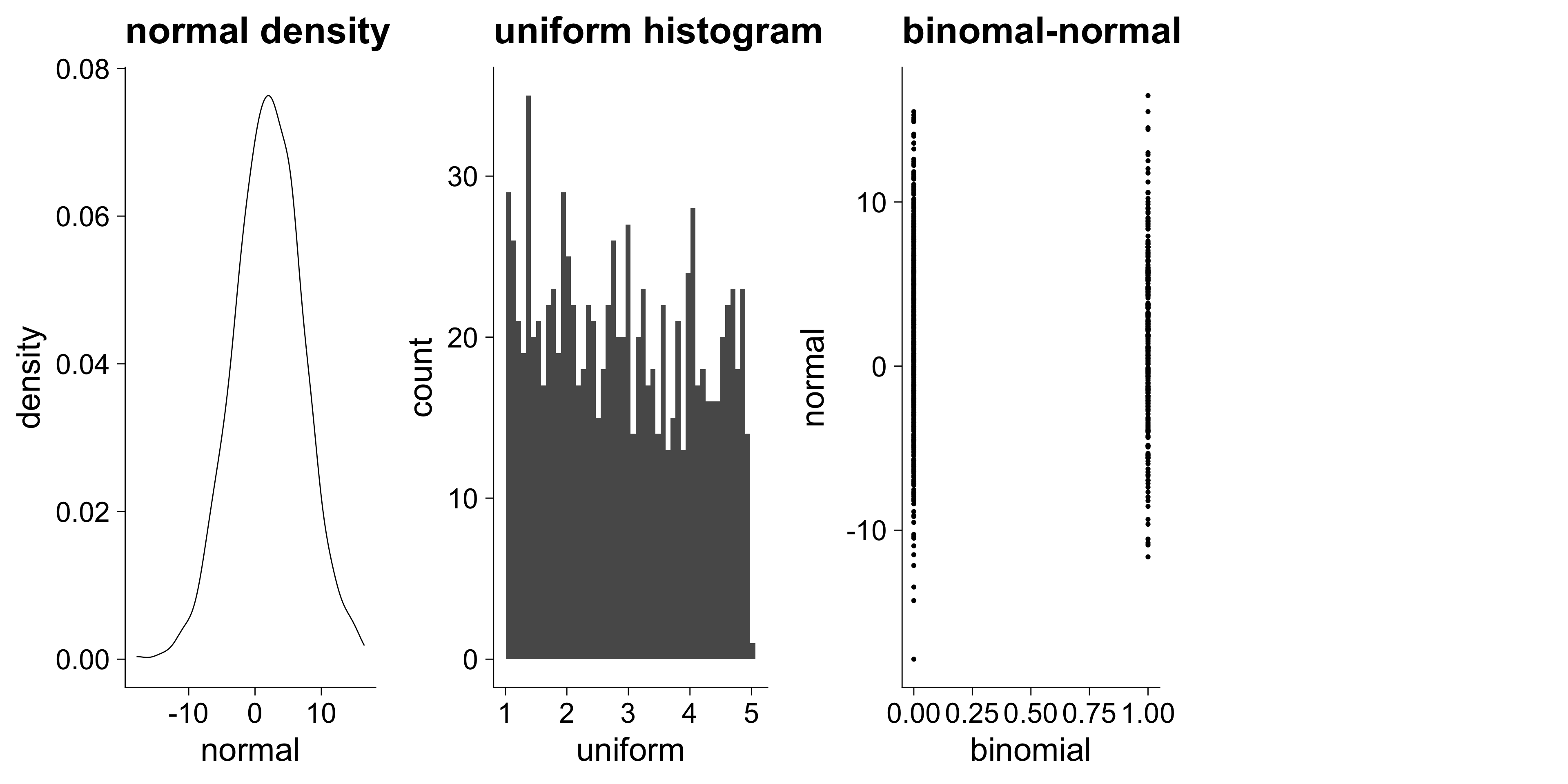
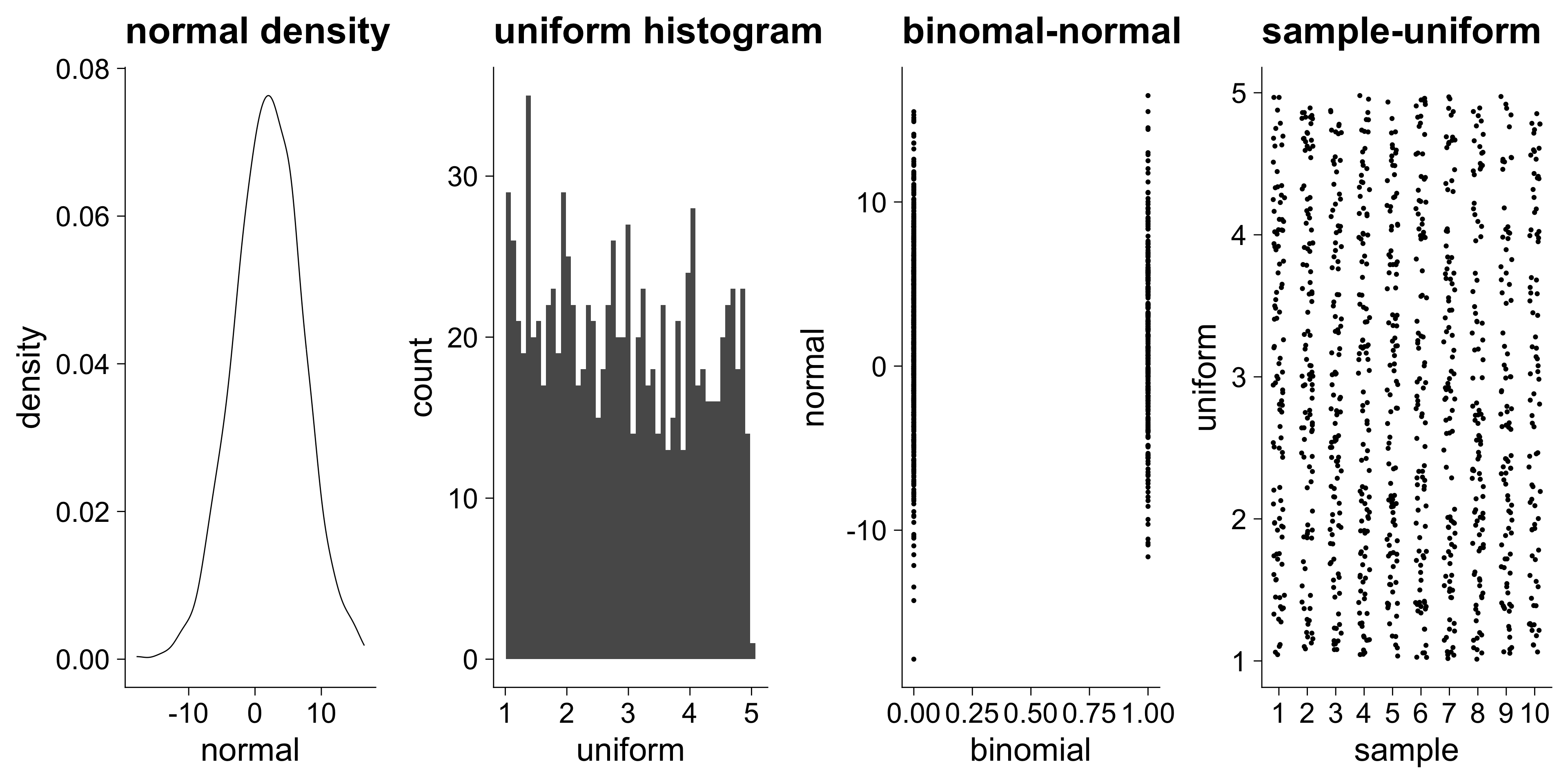
normal = rnorm(N, mean = 2, sd = 5),
uniform = runif(N, min = 1, max = 5),
binomial = rbinom(N, size = 1, prob = .25),
sample = sample(1:10, size = N, replace = T)
)
glimpse(random)Rows: 1,000
Columns: 4
$ normal <dbl> 4.27858718, 2.37025621, 5.19396522, 6.442…
$ uniform <dbl> 1.160221, 2.228684, 2.274665, 1.177478, 3…
$ binomial <int> 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0,…
$ sample <int> 8, 3, 9, 10, 6, 7, 9, 4, 1, 2, 10, 3, 3, …
p1 <- ggplot(random, aes(x = normal)) + geom_density() + ggtitle("normal density")
p2 <- ggplot(random, aes(x = uniform)) + geom_histogram(bins = 50) + ggtitle("uniform histogram")
p3 <- ggplot(random, aes(x = binomial, y = normal)) + geom_point() + ggtitle("binomal-normal")
plot_grid(p1, p2, p3, ncol = 4)
p1 <- ggplot(random, aes(x = normal)) + geom_density() + ggtitle("normal density")
p2 <- ggplot(random, aes(x = uniform)) + geom_histogram(bins = 50) + ggtitle("uniform histogram")
p3 <- ggplot(random, aes(x = binomial, y = normal)) + geom_point() + ggtitle("binomal-normal")
p4 <- ggplot(random, aes(x = as.factor(sample), y = uniform)) + geom_jitter(width = .2) +
ggtitle("sample-uniform") + labs(x = "sample")
plot_grid(p1, p2, p3, p4, ncol = 4)
p1 <- ggplot(random, aes(x = normal)) +
geom_density() +
ggtitle("normal density")
p2 <- ggplot(random, aes(x = uniform)) +
geom_histogram(bins = 50) +
ggtitle("uniform histogram")
p3 <- ggplot(random, aes(x = binomial, y = normal)) +
geom_point() +
ggtitle("binomal-normal")
p4 <- ggplot(random, aes(x = as.factor(sample), y = uniform)) +
geom_jitter(width = .2) +
ggtitle("sample-uniform") + labs(x = "sample")
plot_grid(p1, p2, p3, p4, ncol = 4)Summary
obs <- 500
size_rate <- 1; talent_rate <- 2/3;
C <- 1/60; w0 = 1;
n <- c(1:obs)
size <- 600 * n ^ (-size_rate)
talent <- - 1/talent_rate * n ^ (talent_rate)
wage <- rep(NA, obs)
wage[obs] <- w0
for (i in (obs - 1):1){
wage[i] <- wage[i + 1] + C * size[i + 1] *
(talent[i] - talent[i + 1])
}
matching_plot <- qplot(x = size, y = wage) +
labs(x = "Company Market Value", y = "CEO compensation")
plot(matching_plot + ggtitle("Value - Compensation"))
us_comp <- readRDS(here("data", "us-compensation-new.RDS")) %>%
rename(total_comp = tdc1)
us_value <- readRDS(here("data", "us-value-new.RDS")) %>%
rename(year = fyear, market_value = mkvalt)
summary(us_value$market_value) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
0 976 2794 15560 8934 3522211 3090 _joinus_comp_value <-
select(us_comp, gvkey, year, total_comp) %>%
left_join(
us_value,
by = c("year", "gvkey"))
glimpse(us_comp_value)Rows: 26,574
Columns: 4
$ gvkey <chr> "001004", "001004", "001004", "001004…
$ year <dbl> 2011, 2012, 2013, 2014, 2015, 2016, 2…
$ total_comp <dbl> 5786.400, 4182.832, 5247.779, 5234.64…
$ market_value <dbl> 485.2897, 790.0029, 961.3080, 1046.39…
plot_log <- plot_comp_value +
scale_x_continuous(
trans = "log1p",
breaks = c(1e2, 1e3, 1e4, 1e5, 1e6),
labels = function(x)
prettyNum(x/1000, digits = 2)) +
scale_y_continuous(
trans = "log1p",
breaks = c(1e1, 1e2, 1e3, 1e4, 1e5),
labels = function(x)
prettyNum(x/1000, digits = 2)) +
ylab("compensation ($ million)") +
xlab("market value ($ billion)")
R\[\begin{equation} y_i = a + b_1 x_{1i} + ... + b_n x_{ni} + \epsilon_i \end{equation}\]
\[\begin{equation} \vec{y} = a + b_1 \vec{x_1} + ... b_n \vec{x_n} + \vec{\epsilon} \end{equation}\]
\[\begin{equation} \vec{y} = a + \vec{b} X + \vec{\epsilon} \end{equation}\]
\[\begin{equation} \vec{y} = \mathcal{N}(a + \vec{b} X, \sigma) \end{equation}\]
Our estimates of the pay-performance relation (including pay, options, stockholdings, and dismissal) for chief executive officers indicate that CEO wealth changes $3.25 for every $1,000 change in shareholder wealth (Jensen and Murphy 1990).
[…] The statistic in isolation can present a misleading picture of pay to performance relationships because the denominator - the change in firm value - is so large (Hall and Liebman 1998).
This article addresses four major concerns about the pay of U.S. CEOs: (1) failure to pay for performance; […]. The authors’ main message is that most if not all of these concerns are exaggerated by the popular tendency to focus on the annual income of CEOs (consisting of salary, bonus, and stock and option grants) while ignoring their existing holdings of company equity (Core, Guay, and Thomas 2005).
us_comp <- readRDS(here("data", "us-compensation-new.RDS")) %>%
rename(total_comp = tdc1, shares = shrown_tot_pct) %>%
select(gvkey, execid, year, shares, total_comp)
us_value <- readRDS(here("data", "us-value-new.RDS")) %>%
rename(year = fyear, market_value = mkvalt)
us_comp_value <- left_join(
us_comp, us_value, by = c("year", "gvkey")) %>%
filter(!is.na(market_value) & !(is.na(shares))) %>%
mutate(wealth = shares * market_value / 100)
glimpse(us_comp_value)Rows: 23,138
Columns: 7
$ gvkey <chr> "001004", "001004", "001004", "001004…
$ execid <chr> "09249", "09249", "09249", "09249", "…
$ year <dbl> 2011, 2012, 2013, 2014, 2015, 2016, 2…
$ shares <dbl> 2.964, 2.893, 3.444, 3.877, 4.597, 5.…
$ total_comp <dbl> 5786.400, 4182.832, 5247.779, 5234.64…
$ market_value <dbl> 485.2897, 790.0029, 961.3080, 1046.39…
$ wealth <dbl> 14.383987, 22.854784, 33.107448, 40.5…plot_shares <- ggplot(
data = us_comp_value,
aes(x = market_value/1000, y = shares)) +
geom_point(alpha = .10) +
ylab("CEO Ownership") +
xlab("Firm Market Value (in Billions)") +
scale_x_continuous(
trans = "log",
labels = function(x)
prettyNum(x, digits = 2),
breaks =
scales::log_breaks(n = 5,
base = 10)) +
scale_y_continuous(
trans = "log",
labels =
function(x)
prettyNum(x, digits = 2),
breaks =
scales::log_breaks(n = 5,
base = 10))
us_sens <- us_comp_value %>%
group_by(gvkey, execid) %>%
arrange(year) %>%
mutate(prev_market_value = lag(market_value),
prev_wealth = lag(wealth)) %>%
ungroup() %>%
mutate(change_log_value = log(market_value) - log(prev_market_value),
change_log_wealth = log(wealth) - log(prev_wealth)) %>%
filter(!is.infinite(change_log_wealth)) %>%
arrange(gvkey)plot_hypothesis <- ggplot(
us_sens,
aes(y = change_log_wealth / change_log_value,
x = market_value/1000)) +
geom_point(alpha = .1) +
scale_x_continuous(
trans = "log",
breaks = scales::log_breaks(n = 5, base = 10),
labels = function(x) prettyNum(x, dig = 2)) +
coord_cartesian(
ylim = c(-10, 10)) +
xlab("market value") +
ylab("sensitivity")Definition
Assuming the null hypothesis is true, how likely is it to get an estimate that is as extreme as the one we have in our data.
data_hypo <- us_sens %>%
mutate(
sensitivity = change_log_wealth / change_log_value) %>%
select(sensitivity, market_value) %>%
filter(complete.cases(.))
observed_cor <- cor(
data_hypo$sensitivity, data_hypo$market_value)
random_cor <- cor(
data_hypo$sensitivity, sample(data_hypo$market_value))
print(prettyNum(c(observed_cor, random_cor), dig = 3))[1] "-0.00118" "-0.00296"See also Chapter 4.2 in Cunningham (2021)
